Vibraciones Mecánicas

Movimiento Armónico

El movimiento armónico es importante de estudiar ya que tiene similitud con muchos movimientos de sistemas vibratorios, todo movimiento periódico debe satisfacer:

X (t) = X (t +ζ) EC 3.1

Vamos a ver que significa esto. Un movimiento periódico es un movimiento que se

repite a intervalos de tiempo llamados periodos ‘ζ ’.

La frecuencia se define como el número de ciclos por unidad de tiempo, de tal

forma que se relaciona con el periodo de la forma

F = 1/ζ (EC. 3.2) Las unidades de la ecuación 3.2 son ciclos/seg.

Vibración libre no amortiguada.

En este apartado se estudiara el modelo más simple de tal modo que una ecuación

matemática denotara su comportamiento.

Este modelo lo llamaremos el modelo típico, y la ecuación diferencial que determina

su comportamiento lo llamaremos la forma canónica de un sistema libre no

amortiguado.

La fig. 3.2 muestra este modelo un sistema de masa ‘m’ y una constante elástica ‘k’ vamos a realizar un estudio estático y cinético con el fin de determinar la ecuación diferencial que determinara el movimiento posteriormente veremos la solución de la ecuación diferencial para ver la respuesta en el tiempo del sistema así como la

Formula que determina el cálculo de la frecuencia natural. 

 

 

 

∑ Fy = 0

mg – KXs = 0
mg = Kxs EC.3.3
Ahora imaginemos que estiramos la masa una distancia X y luego lo soltamos y

aquí comenzamos hacer el análisis

 

La figura 3.5 nos muestra el diagrama de cuerpo libre como consideramos X + 1

por lo tanto x y x serán positivos hacia abajo.
Utilizando la 2da ley de Newton
+∑ fy =∑ fyefect = mx
mg – KXt = mx Ec. 3.4
Como KT = Xs + x la ecuación 3.4 se convierte en:
Mg – KXs – Kx = mx Ec 3.5
Utilizando la ecuación 3.3 como en la ecuación 3.5 aparecen como constantes se

pueden eliminar, por lo tanto:

Mx + kx = 0 EC. 3.6

A la ecuación 3.6 se le conoce como la ecuación diferencial del movimiento de un sistema libre no amortiguado. Si existe deformación estática el efecto que produce la masa se coloca con un resorte cuando se deforma estáticamente por lo tanto vamos a buscar la solución utilizando la transformada de Laplace.

Si analizamos el término angular (√K (t)) cuya unidad deberá ser los radianes, por

lo tanto:

√m
√K T = seg.
√m

De aquí que el termino√K es la frecuencia natural en otras unidades

√m

Por lo tanto la EC 3.7 que denota la respuesta en el tiempo del sistema queda:
Determinado su movimiento por la ecuación diferencial:
mx + kx = 0
Cuya solución, queda determinada la respuesta en el tiempo:
x(t) = x(0) cos wnt + x(0) sen wt

Wn
Donde: x (0) = deformación inicial
X (0) = velocidad inicial
wn frecuencia natural (rad/seg.)
La frecuencia natural queda definida como:

Wn =√K /m

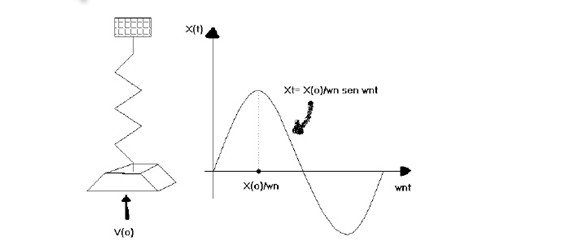
Analizando la ec. 3.11 vamos a analizar su grafica respuesta en el tiempo.

Caso 1 si el sistema parte con velocidad 0; es decir x(0) 

 

 

Puede ser un problema, mas sin embargo solo hay que dedicarse a llegar a la

ecuación diferencial y esta se asemeja a la ecuación 3.6

Definición 3.2.B

Forma canónica de un sistema libre no amortiguado

A+B =0

Donde

= d2 / dt

Re su me n

En general almomento de resolver un problema de vibraciones el

estudiante debe de tener en cuenta las siguientes ecuaciones:

Frecuencia circular natural

ωn= √k/m

Desplazamiento

X= xn sen (ωnt + ø)

Velocidad

V= =xmωncos (ωnt + ø)

Aceleración

a=d2 x/dt = - xmωn2sen(ωnt + ø)

Periodo

ζn =2∏/ ωn

Frecuencia natural

ƒn = 1/ ζn= ωn/2∏

Ej em pl o

Una partícula se mueve en movimiento armónico simple.
Sabiendo que la amplitud es de 18 pulg. y la velocidad
máxima es de 6 m/s, determinar la máxima aceleración de la
partícula y el período de su movimiento.

Solución

18 pulg. = 1.5 m

X =xmsinωnt = 1.5 senωnt

dx/dt = 1.5ωn cosωnt, 1.5ωn = 6m/s

Entonces

ωn = 6/1.5 = 4 Rad. / s = 4/2∏ hz

dx/dt = -1.5ωn2senωn t = - 24 s e nωn t

repuesta
aceleracion maxima = 24 m/s
periodo =∏/2 = 1.5715 s